
分数の割り算はなぜ上下をひっくり返して掛け算なのか
2/3で割るには、3/2を掛けなさいと小学校で習うと思います。
なぜそうなるのか?
そういう風になるように数学の表記方法を誰かが決めたからという以上の理由はありません。
そしてこの表記方法が採用されている理由は、いろいろな場面でその方が都合がよいからです。
もしかしたら上記の問いにもっと賢くこたえられるかもしれませんが、質問の難易度としては『水』はなぜ英語で『water』なのか、と同じくらいだと思います。
それならば御託を並べるよりも、そういうもんだから、と答えておくのがある意味誠実と言えるのではないでしょうか?
無限をとらえることが出来ず高校数学で落ちこぼれる
私は高校時代に150点満点中の10点を数学で取ったことがあります。
数学だけに限らず、私が何らかの新しい概念を理解するときには、そのコンセプトをできる限り可視化して理解を深めるようとする癖があります。
例えば中学校の数学でいうと、未知数がxとyの連立方程式の解はそれぞれの方程式をグラフとして描くと、それらの交点として可視化できるといった具合です。
私はこの可視化にこだわりすぎたため、微分・積分を理解するのに必須である『無限』と『収束する』という概念を高校時代に理解することができませんでした。
無限に小さくしたり、無限に繰り返すという作業を紙の上に可視化することは、当時の私には不可能だったからです。
数学には納得のいかない要素がある
数学は自然現象を記述するのに使われるため、高校生の私はリンゴが地面に向かって落ちるように、数学も自然の一部だと思っていました。
しかし以前にも書いたように数学は人間が作り出した人工言語です。
人工言語であるゆえに多少の不備もあります。
したがって分数の割り算のように時々納得のいかないことも起こります。
例えば、高校数学では以下のように無限回足すといった概念が提示されます。
![]()
なのですが、納得いくでしょうか?(※1)
ちなみに
![]()
なので、1ではありません。(※2)
これらの違いは、上の式の『…』で表した、『おなじパターンで無限に繰り返す』という部分がキーポイントです。
ちなみになぜ、
![]()
となるかというと、分数の割り算の時と同様みんなでそういうことに決めたからです。
そしてそういう風に決めた理由は今のところその方が都合がいいからです。
将来都合が悪くなった場合はどうなるのでしょうか?
その場合は別の表現の仕方を未来の数学者や科学者が考えることになると思います。
数学はそうやって発展してきました。
高校で落ちこぼれることは大した問題ではない
高校数学から少し難しくなる理由の一つとして、私は無限や収束の概念のように、完全には可視化することができないコンセプトが入ってくることがあげられると思います。
そんなときにコンピュータを使うことができると、無限を理解する手助けになると思います。
現在のいかなるコンピュータでも無限回の足し算を行うことはできませんが、百万回の足し算ならば一瞬で行うことができるので、近似的に無限の世界を可視化することができます。
したがって数学につまづいたら、少しプログラミングの勉強をしてみるのはおすすめです。(試しに上の式をコンピュータで計算してみて下さい。)
いろいろと数学と現実世界のギャップを知ることができると思います。
例えば現在のコンピュータの仕組みだと、完全な円をディスプレイに描くことは難しいので、みなさんが日々スマホやPCの画面上で見ている円は、実際には正100角形だったりします。
数学でつまづいたら、コンピュータの助けを使いながら、ちょっと頭の中で空想の世界を広げてみるのがおすすめの勉強方法です。
(※1,2)もう少し数学的に厳密に描くと、
(※1)は
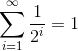
(※2)は
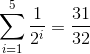
と書くことができます。
↑記事をシェアしてください!読んでいただきありがとうございました。



 慶応大学環境情報学部を首席で卒業。日本のベンチャー企業で働いたのち、アメリカにわたり、カリフォルニア大学バークレー校にて博士号を取得。専攻は機械工学、副専攻はコンピュータサイエンス。卒業後はシリコンバレーの大企業やスタートアップでプログラマとして働いていました。現在はフリーランス。毎日好きなものを作って暮らしてます。
慶応大学環境情報学部を首席で卒業。日本のベンチャー企業で働いたのち、アメリカにわたり、カリフォルニア大学バークレー校にて博士号を取得。専攻は機械工学、副専攻はコンピュータサイエンス。卒業後はシリコンバレーの大企業やスタートアップでプログラマとして働いていました。現在はフリーランス。毎日好きなものを作って暮らしてます。