
誰もが社会の破壊者になるという怖さ
COVID-19への対策の概念を読んだ。
不要不急の外出自粛が求められているのは、自分が感染するのを防ぐためというよりは、自分が感染源になるのを避けるためということが分かった。
COVID-19のクラスター源になり感染を社会に広げるのは感染者のごく一部であるが、軽症や無症状の感染者もそのごく一部のクラスター源になりうるのが厄介だ。
COVID-19は感染しても本人が気がつかない場合がある。
つまり私も含めて、現在特に症状がなくても誰もが感染者である可能性がある。
そしてそんな無症状の自分がクラスターを作ってしまうこともありうる。
だから自分の健康状態に関係なく、できるだけ他人との濃厚接触を避けなければならない。
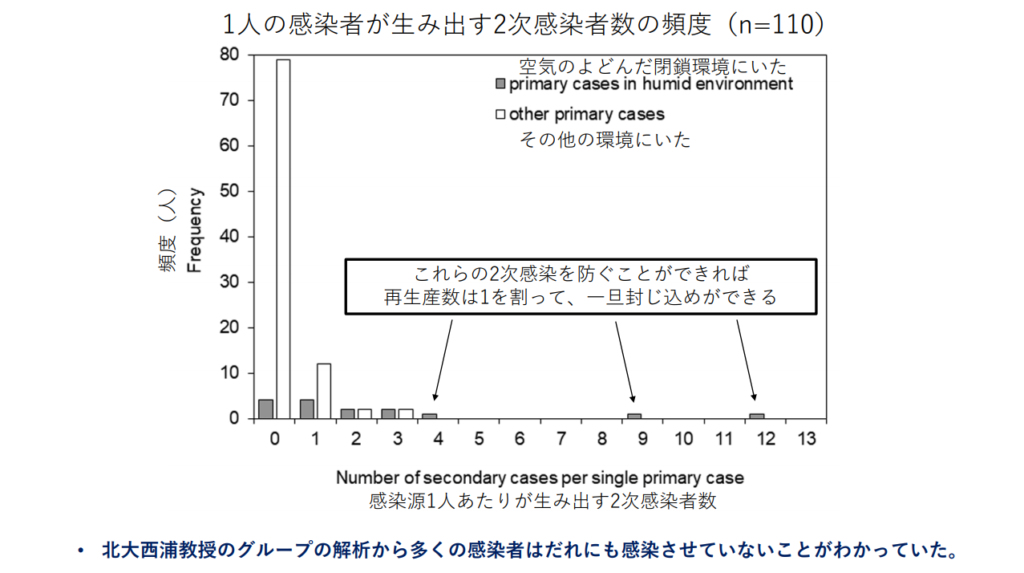
先ほどの資料の21ページ目には、多くの人が他人に感染させることはないが、ごく一部に多くの人に感染させクラスターを作ってしまう人がいることが示されている。
このn = 110のデータの基本再生産係数は
((4+12)*1+(2+2)*2+(2+2)*3+1*4+1* 9+1* 12)/110 = 0.55
n = 110というサンプル数が十分に大きいと仮定するならば、このままいけば封じ込めが可能だということになるが、実際のところはそう簡単ではないのかもしれない。
本当にやばいような気がしてきた
死者数1位と2位であるイタリアやスペインの死者数の推移(Total Coronavirus Deaths)をlogarithmic(対数表示)で見ると、その伸びは鈍化してきているように見える。
逆にアメリカのデータにはその気配がない。
なんとなくExcelでデータを回帰してみることにした。
素人の思い付きでやってみた科学的な根拠ないものなので鵜呑みにしないでください(全く見当違いのおかしな計算をしている可能性があります)。
もし死者数の伸びが指数関数的だと仮定すると、このままの伸びが続けば数日以内に死者数は1万人を超え、2週間後には10万人、20日後には死者数が100万人に届いてしまうかもしれない。
死者数の伸びが多項式で近似できたとしても、伸びが緩やかながら1か月後には死者数が10万人に届いてしまう。
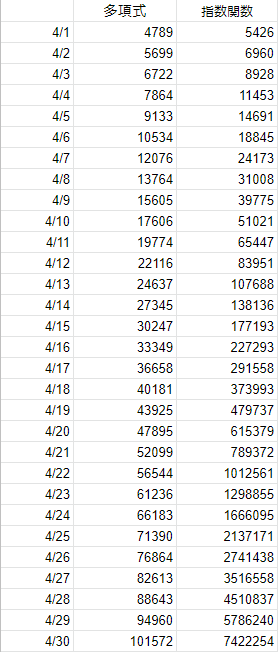
多項式は -40.7+75.5x-14.1x^2+1.12x^3
(R^2 = 0.998)
指数関数の式は 37.3*exp(0.249x)
(R^2 = 0.994)。
xは3月12日からの日数。
今後2週間でアメリカ政府が10万から24万人の死者数を予測しているので、専門家は指数関数的な伸びを想定しているようだ。
上の回帰データだと2週間後の4月16日の予測死者数は17万人なので、プラスマイナス7万人を見積もれば10万人から24万人の予測死者数と一致する。
時代が変わってしまった
先ほどの想定が仮に正しいとしてしまえば、今月末にはアメリカだけでも数百万人単位の死者が出ることになってしまう。
昔から自分の生きている間に大きな戦争や災害に巻き込まれることはあるのかどうかということを考えていた。
東日本大震災を経験しなかった自分は、どうやらこれが一番最初の危機のようだ。
まったく相手が見えないだけにとても不安であり、仮に自分が生き残ったとしても、その後の世界はこれまでとは異なったものになっていくだろう。
自分は早く収束することを願うことと、できるだけ外出を減らすことくらいしかできることはない。
しかし収束したとしても根絶ができなければ、常におびえた状態で暮らすことを余儀なくされることになる。
自分がクラスター源になりうるならば、 疎開のようなことができないのも難しい。
幸い東アジアは被害がまだ目立っていないが、もし仮に大きな被害を被らずに収束した場合でも欧米との断絶は生まれてしまいそうである。
↑記事をシェアしてください!読んでいただきありがとうございました。



 慶応大学環境情報学部を首席で卒業。日本のベンチャー企業で働いたのち、アメリカにわたり、カリフォルニア大学バークレー校にて博士号を取得。専攻は機械工学、副専攻はコンピュータサイエンス。卒業後はシリコンバレーの大企業やスタートアップでプログラマとして働いていました。現在はフリーランス。毎日好きなものを作って暮らしてます。
慶応大学環境情報学部を首席で卒業。日本のベンチャー企業で働いたのち、アメリカにわたり、カリフォルニア大学バークレー校にて博士号を取得。専攻は機械工学、副専攻はコンピュータサイエンス。卒業後はシリコンバレーの大企業やスタートアップでプログラマとして働いていました。現在はフリーランス。毎日好きなものを作って暮らしてます。