
誰もが社会の破壊者になるという怖さ
COVID-19への対策の概念を読んだ。
不要不急の外出自粛が求められているのは、自分が感染するのを防ぐためというよりは、自分が感染源になるのを避けるためということが分かった。
COVID-19のクラスター源になり感染を社会に広げるのは感染者のごく一部であるが、軽症や無症状の感染者もそのごく一部のクラスター源になりうるのが厄介だ。

COVID-19への対策の概念を読んだ。
不要不急の外出自粛が求められているのは、自分が感染するのを防ぐためというよりは、自分が感染源になるのを避けるためということが分かった。
COVID-19のクラスター源になり感染を社会に広げるのは感染者のごく一部であるが、軽症や無症状の感染者もそのごく一部のクラスター源になりうるのが厄介だ。 続きを読む
新井紀子の『AI vs.教科書が読めない子どもたち』が中田敦彦のYouTube大学で紹介されていた。
オリラジが好きなのでよく見ているけど、以前に彼は【AI・人工知能①】〜AIを知れば未来が見えてくる!〜という動画も上げていて、ニューラルネットワークのドロップアウトについて解説するなど、技術的なことにも少し踏み込んだりしていて内容は割といいものだった。
今回はその真逆の新井紀子の本を取り上げているので、中田さんの YouTube大学は本の中身を他の文献と比較して検証したりして解説するものではなく、書いてあることをそのまま読み上げる番組なんだといまさら気が付いた。 続きを読む

本書は4章からなり、最初の2章は『AI』について、後半の2章は『教科書が読めない子どもたちの読解力』について、著者の考えが述べられています。
この投稿は主に最初の2章の『AI』パートのみの書評です。
この本のAIに関する主題を簡単にまとめると、 続きを読む

その究極の理由はムーアの法則、より一般的に言えば絶えることなく指数関数的に計算コストが下がり続けていることにある。
ほとんどのAIの研究は、使用できるコンピュータの計算能力が常に一定(つまり人間の知識を活用することのみがAIの能力を向上させるある意味唯一の方法)であるという仮定の下に行われているが、典型的な研究プロジェクトが行われる期間の間にも、それまでになかったより一層の計算能力が必ず使用可能になる。
短期的にAIの能力を向上させるために、研究者はそれぞれの分野における人間の知識を活用する方法を模索するが、長期的に違いを生むのはコンピュータの計算能力のみである。 続きを読む

これは先日私が撮った写真です。
エスカレーターの右側ががら空きなのにも関わらず、左側に立つために待っている人の行列ができています。
これは駅などでよく見る光景ですが、人を捌く機械としてエスカレーターを見た場合、効率が悪いと以前から感じていました。
(うまく表示されされない方はこちら)
window.onload = function() {
// alert(document.getElementById("frame_test").offsetWidth + " " + document.getElementById("test1").offsetWidth + " " + document.getElementById("test2").offsetWidth);
let container_width = parseInt(document.getElementById("test2").offsetWidth, 10);
document.getElementById("frame_test").src = "https://mywarstory.tokyo/my-code/escalator.php#" + container_width;
};
立ちたい人が赤、歩きたい人が青です。
歩きたい人の割合をスライダーで決めて、『シミュレーション開始』ボタンでシミュレーションが始まります。
左のエスカレーターが片側立ち、右のエスカレーターが両側立ちのシミュレーションです。
100人の立ちたい人と歩きたい人がランダムに配置された行列が、エスカレーターに乗っていく様子が観察できると思います。
これができれば、行列が形成されにくくなります。(例えば通勤ラッシュ時の駅のホームでは、いかにプラットホームからエスカレーターに早く人を流し、続いて到着する電車の乗客のための空間をできるだけ多く作ることが大切と考えられます。)
シミュレーションでは、行列の中の歩きたい人の割合に関わらず、両側立ちの方が常に早く行列が解消されるのが観察できるはずです。
例えば、歩きたい人の割合を25%に設定しシミュレーションをすると、行列の後ろの方にいる歩きたい人は、意外にも両側立ちの方が早くエスカレーターの向こう側にたどりつけることが観察できます。
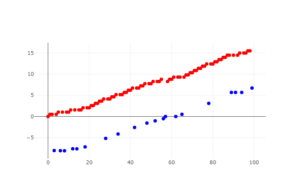
このグラフは、両側立ちの時に、片側立ちの時と比べて、何秒早くエスカレーターの向こう側にたどりつけたかをプロットしたものです。
横軸は行列の中の順番、縦軸が何秒早くだどりつけたかを示しています。
シミュレーションと同じように、赤い点は立ちたい人、青い点は歩きたい人に対応します。
赤い点の縦軸の値は常にプラス、つまり立ちたい人にとっては、常に両側立ちの方が早くエスカレーターの向こう側にたどり着けることがわかります。
特にグラフが右肩上がりであることから、行列の後ろに並んでいる人ほどその恩恵を多く受けることがわかります。
歩きたい人にとっては、行列の先頭の方にいると縦軸の値がマイナス、つまり両側立ちを強制されることによってエスカレーターの向こう側にたどり着く時間が遅くなります。
しかしこのグラフで注目するべきは、大体60番目以降にいた歩きたい人たちは、両側立ちを強制されることによって早くエスカレータの向こう側にたどりつけるということです。
なぜなら両側立ちをすることで行列の解消が早まるので、先を急いでエスカレータを歩きたい人も恩恵をうけることがあるからです。
歩きたい人はこれまで通り、前が空いている限り歩くのがいいと思います。
立ちたい人は左右関係なく空いているところに立ってしまう方が全体の効率を高めます。
混んでいるエスカレータは両側立ちの方がいいと思います。(前が空いている場合は歩きたい人は歩いて問題なしです。)
都内近郊の駅でエスカレーターに並ぶ行列を見ていると、立ちたい人は初めから左側に、歩きたい人は初めから右側に列を作っているようです。
この習慣を活かして、まず最初はこれまで通り片側立ちをします。
そうすると大抵は右側の歩きたい人たちの行列が先に解消されるはずです。
その後は左側に行列を作っている人たちは、エスカレーターの左側だけでなく右側にも立てば(つまり両側立ちをすることで)、割と誰も損せずに全体としての効率が上がるのではないかと思います。
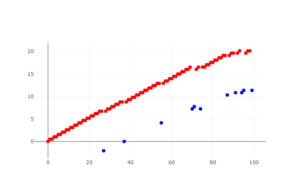
(歩きたい人の割合: 10%)
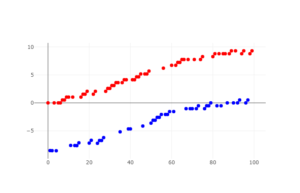
(歩きたい人の割合: 50%) 続きを読む
研究というものに関わり始めたのは、私が20歳であった2002年頃でした。
その時のテーマは先生の言われるがままにGPGPUに関するものでした。
決まった処理しか行うことのできなかったGPUがプログラム可能になり、かつ32ビットのデータを扱うことができるようになったことにより、GPUをグラフィックス以外の処理に用いて計算の高速化をしようという雰囲気が生まれていたころです。
まだ当時は短いプログラムしか実行できず、またGPUでのプログラミングはCPUのそれと比較して面倒であり、私はあまりGPUプログラミングが好きではありませんでした。
特に当時は『CPUからGPUに処理を移すことで得られる計算速度向上』が、すべてCPUで計算していれば必要のない『CPUとGPU間のデータ転送速度の遅さ』に簡単に食われてしまい、全体として計算速度が上がった感じがいまいちしなかったのも好きでなかった要因です。
できるだけCPUとGPU間のデータ転送をなくすような方法を考えるといった、かなり地道な作業がGPUの処理速度を活かすには必要で、これをやっていてもあまり未来がないような感じもしていました。
また具体的には誰だったか忘れましたが、当時high-performance computingで有名な大学の先生も、将来的にはGPGPUは来ないだろうと予測して、私の指導教官が軽くショックを受けていたのも覚えています。
しかし15年ほどたった現時点でこの予測は外れています。
現在では例えばCPU上で動く画像処理のプログラムを、そのまま何の工夫もせずにGPUに移植するだけでCPUで計算するのが馬鹿馬鹿しいくらいに処理速度が上がります。
GPUがいくら早くなろうとも中毒的なゲーマーにしかその恩恵が感じられなかったのも今は昔で、GPGPUは機械学習という応用分野で産業とつながり、仮想通貨のマイニングによる需要急増のために本来GPUを必要としているグラフィックスアーティストやプログラマがGPUの在庫不足による値段の高騰を嘆く、といった状況が来るとは10年前には誰も想像できなかったと思います。
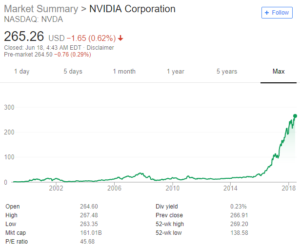
同じ2003年頃、私はニューラルネットワークという科目を大学で履修しました。
排他的論理和のような離散的な論理演算を連続的な関数を組み合わせることで表現できるなど、その不思議さにとても魅了されたのを覚えています。
授業の最後のプロジェクトではこちらのお絵描きパズルを自動で解くプログラムと、自動着色のプログラムを書いてみました。
ニューラルネットワーク自体が非常に強力であることは今では疑いのない事実ですが、これに関しても当時とあるアメリカのコンピュータビジョンの研究者が、自著でニューラルネットワークは来ないだろうと書いていたのを覚えています。
先ほどのGPUの話もそうですが、どんな分野が産業界で花開くかを予測するのは専門家にもとても難しいのだと思います。
私が初めて渡米した2006年頃はスマホは世界に存在せず、日本の携帯電話は格好いい携帯電話でした。
また当時の人々が描く未来のコンピュータの利用方法は、現在でも主流であるアプリをクライアント側(スマホやコンピュータ)にダウンロードするのではなく、クラウド側にアプリケーションを置き、クライアント側はただのユーザーインターフェースになるだろう、というものだったのを覚えています。
私自身もネットワークの速度やコストがボトルネックにならなくなるにつれて、そのスタイルがより未来的だと思っていました。
しかしiPhoneの登場はその流れを完全に断ち切った感があります。
スマホでの処理はブラウザ上で行うのではなく、アプリを介して行うのが今では主流です。
しかし2014年のHTML5の登場により、GPUを用いた処理がブラウザ上でも容易になり、この流れは数年後にまた変わるかもしれません。
また2018年現在、コンピュータサイエンスはその技術者の待遇を含めてとても花のある分野ですが、何度か書いていますが私が学生だった2000年初頭の日本ではそうではありませんでした。
当時は『プログラマ=技術に興味のない人たちに振り回される徹夜・休日出勤を強いられるIT土方』であり、東京大学でも情報工学に進学する学生が減っていると先生が嘆いていたのを覚えています。(現在はどうなのでしょうか?)
当時の私自身は、自分のやっていることはもっといいもののはずだという気持ちがありました。
このまま日本にいてもいいことなさそうだなと思ったのは、私がアメリカに行くことにした理由の一つです。
Twitterを見ていると日本のプログラマを取り巻く環境もだいぶよくなってきたような印象がありますが、みなさまいかがでしょうか?
日本のプログラマの皆さまが幸せな毎日を過ごしていることを願っております。
新井紀子教授はAIの専門家ではない 『AI vs. 教科書が読めない子どもたち』という記事を書いて約一か月が経ちました。
15000人の目に触れたようなので、いろいろなコメントをもらっています。
まずははてなから。
氏には首肯し難い主張が多いが、これはブログ主の誤解。氏の主張は「各頂点からの距離の和が一番小さくなる点」が対角線の交点になることの数学的証明がスパコンに困難という話。対角線の交点自体は当然計算可能。
私が書いたプログラムが『単に対角線の交点を計算しているだけ』と勘違いしている人が多いのは私の書き方が悪いのでしょうか?
『このプログラムはGeometric medianが対角線上に存在するということはもちろん知らずに、あなたのコンピュータやスマホ上でリアルタイムにそれを見つけだしています。』と元記事では『もちろん知らず』を強調しておいたのですが、これで伝わらないとなるとコミュ障の私には厳しいです。
また、あの文章をどう読めば『証明しなければいけない』という解釈になるのかいまだに理解できないです。
新井紀子教授が提案するリーディングスキルテストです。
匿名なのでよかったら回答してみてください。
問題はこちら。https://t.co/Y5UPdoMjSp
— yu. (@yu_phd) March 16, 2018
正直、答えが分かりません。数学的には2つの選択肢は同じ意味だと思います。
— Willy 🌔米国大学教員 (@willyoes) March 19, 2018
Willyさんありがとうございます。
そもそも実際に問題が解けていることが確認できる時点で、エンジニアリング的には証明をする必要が見出せません。
時速100㎞で走っている車を目の前にして、その車が時速100㎞で走る能力があることを証明しろと主張することに意味があるのでしょうか?
計算量O(n)の極大化の話題に対してアルゴリズムによる計算量の極小化をもって解決可能!と主張してる。なんと言うか、ブログ主のコミュニケーション能力は極小だな。
何を言っているのか意味不明です。適当なテクニカルタームを並べて何か言った気になるのは、わかる人から見ると、残念な人に見えるだけなのでやめた方がいいと思います。
そもそもの主張の誤解もそうだしヒューリスティクスの説明もひどいし遺伝的アルゴリズムの例示も不適切(この場合は実質二分法で適当な仮定の下で確率1で収束してしまう)、新井先生はさすがにもうちょっとまともですよ
1次元の連続関数の解を見つけるアルゴリズムである二分法を、2次元の問題にどのように適用するのか具体的に説明してほしいです。そもそもが『距離の和が一番小さくなる点』を求めるのに論理も確率も統計も必要ないというのが趣旨なので、それをくみ取っていただかないで適当な仮定の下で云々とかいわれても困ります。
私としては、新井紀子教授が実用的なプログラムを書いたことがない人だというのは彼女の書籍を読めば一目瞭然だと思います。
しかし世の中の人誰もがプログラマではないですし、一口にプログラマと言ってもIT土方と呼ばれる人から、世界中で使われるAI関連のオープンソースソフトウェアを開発する人までピンキリなので、それを判断するのは多くの人にとってとても難しいということがわかりました。
私も新井紀子教授はもう少しまともな人だと思っていましたが、残念ながら彼女が根本的に理系の教養がない人だというエピソードを見つけてしまいました。
新井紀子著『こんどこそ! よくわかる数学』より引用です。(元ネタはこちら)
ガリレオのピサの斜塔での実験では, 重い鉛の玉も軽いアルミニウムの球も同じように落ちて, 同時に地面に着きます. 重さは落ちる速度には関係なく, どんなものでも落としてから1秒後には落下の速度は秒速9.8メートルになり, 2秒後には秒速19.6メートルになります. つまり, 1秒ごとに秒速9.8メートルずつ速度が上がるのです. x秒後の秒速yを式で表すと, y=9.8x(m/秒)となります.
y=9.8x(m/秒)の解釈が『1秒ごとに秒速9.8メートルずつ速度が上がる』というのは数学を持ち出すまでもなく物理的におかしいでしょう。
そんな奇妙な加速をしながら落下する玉を私は見たことがありません。
この本は中高生向けの本なのですが、読解力のある中高生はこの文章を読むと間違った知識を手に入れることになります。
なんとなく『1秒ごとに秒速9.8メートルずつ速度が上がる玉』が、どのような動きなのか気になったので以下にプログラムを書いてみました。
新井紀子教授の世界(Norico’s World)を私たちの世界(Our World)と合わせてご覧ください。
Norico’s Worldの玉の動きは明らかに私たちが地球上で観察する玉の動きと似ていません。
なぜこのようなおかしなことが起こるかというと、新井紀子教授の科学に対する姿勢は以下の通りだからです。
数学さえ分かっていれば、AIに何ができるか、そして何ができないはずかは、実物を見なくてもある程度想像がつくのです。(『AI vs. 教科書が読めない子どもたち』より引用)
脳内で勝手に想像するのはご自由ですが、それをもって現実世界を断定するのは博士号を持つ大学教授の姿勢としては非常に問題のある態度です。
新井紀子教授は数式を見て勝手に間違った判断を下すのではなく、もう少し現実世界を観察し、実物を見て、自分の理解が正しいか確かめた方がいいと思います。
そもそも実物を見ようとしない研究者に存在価値などあるのでしょうか?
これは人間が導いた答えを分かりやすく表示するプログラムを作りましたということですか? 続きを読む
ご覧になっていない方はまずこちらからお読みになってください。
=&0=&
私は本書を読んで、新井紀子教授が何を勘違いしているのか理解できました。
引用では省略しましたが、ここでいう『それらの画像』とはMRIやマンモグラフィのことです。
そしてここでいう『規格』とは、『どのような手法で画像を取得するか?』ということだと推測できます。MRIを使うかX線を使うかで、まったく同じものを撮影しても取得できる画像が異なるからです。
つまりここでは『撮影方法』の規格の話をしているのに、新井紀子教授はそれを『ピクセル行列で表された画像の表現方法』に異なる規格があると勘違いしているのです。
犬の写真とかいう見当違いの例を出しているのが何も理解していない証拠です。
ピクセルデータはどこまで行ってもピクセルデータです。
スマホのカメラで撮影した犬の写真を見て、それを撮ったスマホのメーカーやモデルを当てることは普通出来ないでしょう。
ピクセルデータには異なる規格という概念はありません。
新井紀子教授が画像処理のプログラムなど一度も書いたことがないのがよくわかるエピソードです。
画像認識や音声認識の最前線で戦っている何人もの優秀な研究者から直接確認したことですから間違いありません。
その研究者の方々の言っていることは正しいと思います。
間違っているのは新井紀子教授の解釈です。
また解像度が変わっただけで、学習したディープラーニングモデルが使えなくなるようでは実用に耐えません。
この問題に対するもっともシンプルかつ効果的な対応方法は、元画像だけでなく、それを拡大縮小させた画像も一緒に学習データの中に入れておくことです。(Data augmentationといいます)
実は新井紀子教授はこの問題に対する対応方法を本書の中で自分で書いています。
回転しても拡大縮小してもやはりイチゴはイチゴで、解像度を下げてもやはりイチゴです。何を当たり前なことを、と思われるかもしれませんが、ここがとても重要なのです。膨大な教師データを作成しようとすると、普通ならとてつもないコストがかかります。でも、画像の場合は、一枚の教師データを回転したり拡大縮小したりすることで、教師データの数は一気に増えます。業界ではこれを「水増し」と呼んでいます。
これはまさに入力画像の解像度が変わっても学習モデルがうまく動くようにするための処理です。
しかし新井紀子教授はこれを水増しとよび、単に教師データ数を増やすための処理だと間違った解釈をしています。
『直接確認したことですから間違いありません』という言葉が先ほど出てきました。
専門家が言っているから信じるというのは良くない習慣です。特に博士号を持つ大学教授が言うべき言葉ではありません。
『聞いたから~だ』だと主張するのではなく、わからないものはわからないと素直に言えばいいと思います。
世の中のすべてのことに精通している人など誰もいないので、別に知らないことは恥ずかしいことでもないですし、もちろん悪いことでもありません。
むしろ博士や大学教授の言うことは正しいと思い込んでいる方は少なくないので、数学者や大学教授という肩書で間違った情報を流すのは社会にとって有害です。
今はだれでも最新の研究成果が記された論文に無料でアクセスできます。
自分が大切だと思うことに関しては、新聞やニュースなどの『伝聞の伝聞』を聞いて分かった気になるのではなく、できるだけ現場の人間が出している情報に直接あたることを意識する必要があります。
『AI vs. 教科書が読めない子どもたち』は、子供たちの読解力を向上を目指すためにリーディングスキルテストを中学1年生全員に受験させるたいという言葉で結ばれます。
読解力はあるにこしたことはないと思いますが、私は十分な知識が伴わない単なる読解力は有害になることも多いと考えています。
新聞に書いてあることは常に鵜呑みにするべきですか?と問われれば、私の言っていることは理解していただけるのではないかと思います。
AIのどこが気に入らないか、今言葉になった。
AIは短期的には多くの人の「役に立つ」けど、長期的にはほんの一握りの人の巨大な利益をもたらし、圧倒的多くの人から搾取する装置(戦争で犠牲になることも含めて)だから気に入らないのだ。
— 新井紀子/ Noriko Arai (@noricoco) March 8, 2018
読解力があっても、書いてある内容を自分の知識と照らし合わせてその真偽を判断できなければ、他人に簡単にコントロールされてしまいます。
読解力も大切ですが、それ以上に、自分の手を動かし、自分の目で見て知識と経験を増やし、自分で真偽が判断できる部分を増やすことこそが、もっとも人生を楽にするものだと私は考えています。
そのためには知識と経験がなによりも大事で、そのスタート地点に立つための準備が学校の勉強です。
新井紀子教授の『AI vs. 教科書が読めない子どもたち』という本が大変売れているようです。
私も本を購入し精読させていただきました。
一言で感想を言うと、新井紀子教授のAI技術に関する知識はせいぜいAI関連ニュースに詳しい人レベルであり、そのベースであるコンピュータに関する知識もほぼ素人だということがわかりました。
『AI vs. 教科書が読めない子どもたち』で彼女が描く未来のビジョンに共感するかどうかは読者それぞれの自由ですが、彼女のことをAI技術に関する専門家だと勘違いしている方が多いのは問題があると私は考え、こちらの記事を書くことにしました。
『AI vs. 教科書が読めない子どもたち』からの引用です。
コンピュータはすべて数学でできています。AIは単なるソフトウェアですから、やはり数学だけで出来ています。数学さえ分かっていれば、AIに何ができるか、そして何ができないはずかは、実物を見なくてもある程度想像がつくのです。(中略)
論理、確率、統計。これが4000年以上の数学の歴史で発見された数学の言葉のすべてです。そして、それが、科学で使える言葉のすべてです。(中略)コンピューターが使えるのは、この3つの言葉だけです。
『コンピュータが使えるのは論理、確率、統計だけ』という主張は正しくありません。
私はエンジニアなので、口で言うだけではなく、誰にも客観的にわかる形で彼女の主張が間違っていることを示す一例を紹介します。
『AI vs. 教科書が読めない子どもたち』には以下のようなエピソードが出てきます。
「平面上に四角形がある。各頂点からの距離の和が一番小さくなる点を求めよ」
実際に図を描いてみるとわかりますが、人間だったら、「答は、対角線の交点だな」となんとなくわかります。証明もそれほど難しくありません。(中略)
先ほどの四角形の問題をコンピューターに解かせてみようとしたところ、いつまでたっても応答がありません。知人にお願いしてスパコンを使ってみたのですが同じ結果です。そこで理論計算をしてみました。すると、宇宙が始まってから現在までよりも長い時間を要することがわかりました。
これは数学的にいうと、四角形の頂点のGeometric medianを求めるという問題です。
以下の図では、白い線で表した四角形のGeometric medianを赤い点で表しています。

左の図のようにすべての頂点の角度が180度より小さい場合は、黄色で示した対角線の交点がGeometric medianになります。
右の図のように角度が180度より大きい頂点がある時は、その頂点がGeometric medianになります。
新井紀子教授は、人間は簡単に四角形のGeometric medianを見つけることができるが、その点が対角線上にあることを知らないコンピュータは、スパコンを用いても現実的にそれを見つけることはできないと主張しています。
しかしこれは明らかに間違っています。
以下に四角形のGeometric medianをリアルタイムで計算するプログラムを書いたので、ぜひあなたの目で確かめてください。
四角形がどのような形になろうとも、Geometric medianを示す赤い点は、常に対角線上(もしくは角度が180度より大きい頂点がある場合はその頂点上)にあるはずです。
このプログラムはGeometric medianが対角線上に存在するということはもちろん知らずに、あなたのコンピュータやスマホ上でリアルタイムにそれを見つけだしています。(追記:誤解されている方が多いようですが、黄色で示した対角線はみなさん人間が結果を検証しやすいように表示しているだけです。)
誰でも確認ができるJavascriptのコードなので、プログラムに興味がありPCやMacから見ている方はこちらから実際のソースコードを確認してみてください。(スマホからアクセスしている方はこちら)
人間と異なりコンピュータプログラムは嘘がつけません。
wikipediaによると、『Geometric medianを数学的に表す公式が存在しない』ことはすでに証明されているようです。しかしそのような問題も、コンピュータを使うとこのようにスマホ上でも一瞬で解くことができます。
数学的に解けない問題でもコンピュータは解ける、つまり『コンピュータはすべて数学で出来ている』というのは間違っているということです。
ちなみに、このGeometric medianの例は、各頂点からの距離の和が最小になる点を探すのが目的ですが、『何かを最小化する点を探す』というのはコンピュータで最もよく扱われる処理の一つです。
それに気がつかず、数学的に無理ならばコンピュータでも無理だろうと単純に考えてしまった新井紀子教授は、人生で一度もコンピュータを使って問題を解決したことがないとしか思えません。
Heuristicとはものすごく雑に言ってしまえば『試行錯誤で解く』ということです。
コンピュータのすごいところは、数学的・論理的に解けない問題でも、その圧倒的な処理量を用いて試行錯誤で答えを探し出すことができることです。
上記で私が示したプログラムはHeuristicの一つである『遺伝的アルゴリズム』という手法を用いています。ダーウィンの自然選択説に着想を得た手法です。
遺伝的アルゴリズムは数学理論に基づいていませんし、論理でも確率でも統計でもありません。
wikipediaの『遺伝的アルゴリズム(Genetic algorithm)』からの引用を訳します。(カッコ内はオリジナルの英文です。)
遺伝的アルゴリズムは簡単に実行できるが、その振る舞いを理解するのは難しい。特に遺伝的アルゴリズムが実用的な問題に対して使われたときに、なぜ多くの場合に高精度な答えを導き出すのかを理解するのは難しい。
(Genetic algorithms are simple to implement, but their behavior is difficult to understand. In particular it is difficult to understand why these algorithms frequently succeed at generating solutions of high fitness when applied to practical problems.)
例えば 5x + 3 = 9 という方程式が与えられた場合、中学校では以下のような手順でxの値を求めるように習うと思います。
5x + 3 = 9 ⇒ 5x = 6 ⇒ x = 1.2
これは数学的にとても論理的なアプローチです。
一方でHeuristicの一つである遺伝的アルゴリズムは、例えば以下のような手順で5x + 3 = 9を求めます。
まず第一世代として、100個のランダムな数を生成する。
人間がやったら日が暮れてしまうようなアプローチですが、コンピュータはこのような作業を一瞬でやりとげ、答えにたどり着きます。
天気予報や空気抵抗を考慮した新幹線の形状の設計など、現実の世界で私たちが解きたい方程式は、多くの場合数学の公式だけを用いて解くことはできません。
そこでコンピュータの助けを借りてHeuristicに問題を解くのです。
Heuristicは数学的とも論理的とも言えないアプローチですし、答えにたどり着くという保証もありません。
でもなぜかうまくいくのです。
人間は四角形の頂点のGeometric medianが対角線上にあることを知っていますが、五角形や六角形や、100角形のGeometric medianがどこにあるかを知ることはできません。
しかし先ほど示した私が30分で書いた50行にも満たないプログラムは、1000角形のGeometric medianもHeuristicに一瞬で見つけてくれます。
人間から見たら賢くないアプローチでも、それを超高速でこなすことで、人間が数学を駆使しても辿り着くことのできない答えにたどりくことができるのがコンピュータの強みです。
こちらはリアルタイムに八角形のGeometric medianを見つけるプログラムです。
もはや人間にはこのプログラムが正しい答えを出力しているのかどうかすらわからないでしょう。
しかしコンピュータは淡々と答えを導き出しつづけるのです。
関連記事:

日本人男性にとってバレンタインデーとは受け身で過ごす一日だと思いますが、アメリカにおけるバレンタインデーはカップル双方にとってとても大切な一日です。
気分としては、日本のクリスマスに近いと思います。
アメリカ人にとっては、バレンタインデーこそがカップルで過ごさないと寂しいと感じる一日なのです。 続きを読む